Question

I need help with my practice test questions . Can you tell me if I got question 2 right ?

Answer 1

Given:

The objective is to find the exact value of sin(285°).

Step-by-step explanation:

The given value can be rewritten as,

`\sin 285\degree=\sin (240\degree+45\degree)\text{ . . . . (1)}`

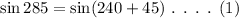
The general formula of sin(a+b) is,

`\sin (A+B)=\sin A\cos B+\sin B\cos A\text{ . }\ldots\text{ .(2)}`

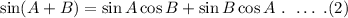
Here A = 240° and B = 45°.

Using equation (2), the equation (1) can be written as,

`\begin{gathered} \sin (240\degree+45\degree)=\sin 240\degree\cos 45\degree+\sin 45\degree\cos 240\degree \\ =\sin (180\degree+60\degree)\cos 45\degree+\sin 45\degree\cos (180\degree+60\degree)\text{ .. .. . . }\ldots\text{ (3)} \end{gathered}`

Since it is known that,

`\begin{gathered} \sin (180\degree+60\degree)=-\sin 60\degree \\ \cos (180\degree+60\degree)=-\cos 60\degree \end{gathered}`

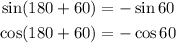
Now, equation (3) can be written as,

`\sin (240\degree+45\degree)=-\sin 60\degree\cos 45\degree+\sin 45\degree(-\cos 60\degree)\text{ . . .. . (4)}`

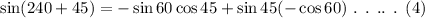
On plugging the trigonometric values in equation (4),

`\begin{gathered} \sin (240\degree+45\degree)=(-\frac{\sqrt[]{3}}{2}*\frac{1}{\sqrt[]{2}})+(\frac{1}{\sqrt[]{2}}*-(1)/(2)) \\ =-\frac{\sqrt[]{3}}{2\sqrt[]{2}}-\frac{1}{2\sqrt[]{2}} \\ =-\frac{\sqrt[]{3}}{2\sqrt[]{2}}*\frac{\sqrt[]{2}}{\sqrt[]{2}}-\frac{1}{2\sqrt[]{2}}*\frac{\sqrt[]{2}}{\sqrt[]{2}} \\ =-\frac{\sqrt[]{6}}{4}-\frac{\sqrt[]{2}}{4} \\ =\frac{-\sqrt[]{6}-\sqrt[]{2}}{4} \end{gathered}`

Hence, option (1) is the correct answer.