Question

The following graph describes function 1, and the equation below it describes function 2. Determine which function has a greater maximum value, andprovide the ordered pairF(x)=-x^2+2x-15

Answer 1

To answer this question, we need to observe with attention the vertex for each function. This is the maximum value for a parabola. Then, we can determine the maximum for the function on the graph, and then we can determine algebraically the vertex for the second function.

First Case: Graphed Function

We have the graph of this function as follows:

If we identify the vertex for this function, we can see that the vertex is the point x = 4, and y = 1 or (4, 1).

Second Case: The function -x²+2x-15

We can use the vertex formula for a parabola as follows:

`x_v=-(b)/(2a),y_v=c-(b^2)/(4a)`

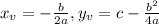
This formula is for a parabola equation of the form:

`ax^2+bx+c`

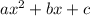
Since we have the function:

`-x^2+2x-15^{}`

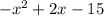
Then, we have that:

`a=-1,b=2,c=-15`

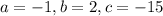
Therefore, the vertex is:

`x_v=-(b)/(2a)\Rightarrow x_v=-(2)/(2(-1))\Rightarrow x_v=-(2)/(-2)\Rightarrow x_v=1`

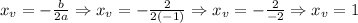
And the y-value is:

`y_v=c-(b^2)/(4a)\Rightarrow\begin{cases}a=-1 \\ b=2 \\ c=-15\end{cases}`
`y_v=-15-(2^2)/(4(-1))=-15-(4)/(-4)=-15+(4)/(4)=-15+1=-14`

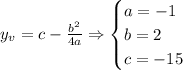
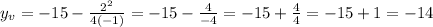
Then, the vertex is (1, -14).

If we compare the two functions, we have:

• The vertex of function 1 is (4, 1).

,

• The vertex of function 2 is (1, -14).

In summary, therefore, the function that has a greater maximum value is function 1 [the value for the vertex is (4, 1)].