Question

Solve the rational inequality. Express your answer in interval notation

Answer 1

Procedure

A rational inequality is an inequality that contains a rational expression.

Step 1. Write the inequality as one quotient on the left and zero on the right.

`(x-3)/(x+2)\le0`

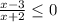
Step 2. Determine the critical points—the points where the rational expression will be zero or undefined.

The rational expression will be zero when the numerator is zero. x = 3

The rational expression will be undefined when the denominator is zero. x = .2

The critical points are -2 and 3

Step 3. Use the critical points to divide the number line into intervals.

`(-\infty,-2),(-2,3\rbrack,\lbrack3,\infty)`

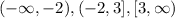
Step 4. Test a value in each interval.

To find the sign of each factor in an interval, we choose any point in that interval and use it as a test point.

Solution

[tex]\begin{gathered} -2