Question

Suppose a population of rare frogs is dying off at a rate such that half the population is gone every 25 years. How many years will it take for the population of frogs to fall to 10% of what it is today?

Answer 1

In order to calculate the amount of time needed, we can use the formula below:

`P=P_0\cdot(1+r)^{(t)/(n)}`

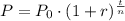
Where P is the population after t years, P0 is the initial population, r is the rate and n is the period of half-life.

So, for P = 0.1*P0, r = -0.5 (the population decreases by half its amount) and n = 25, we have:

`\begin{gathered} 0.1P_0=P_0(1-0.5)^(t/25) \\ 0.1=0.5^(t/25) \\ \log (0.1)=\log (0.5^(t/25)) \\ \log (0.1)=(t)/(25)\log (0.5) \\ (t)/(25)=(\log (0.1))/(\log (0.5)) \\ (t)/(25)=(-1)/(-0.301) \\ (t)/(25)=3.322 \\ t=83 \end{gathered}`

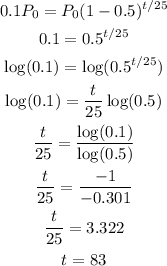
Therefore it will take approximately 83 years.