Given the function:
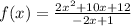
You know that it is a Rational Function because it has the following form:
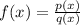
Where the numerator and the denominator are polynomials and:
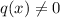
By definition, an Asymptote is a line that the function approaches but it does not touch it and it does not intersect.
To find the Vertical Asymptote, you can follow these steps:
1. Take the denominator of the function and make it equal to zero.
2. Solve for "x".
Then, the Vertical Asymptote is:

To find the Horizontal Asymptote, you can follow these steps:
1. Identify the numerator of the function:

2. Identify its denominator:
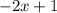
3. Identify the degree of the numerator and the degree of the denominator:
- Since the highest exponent of the numerator is 2:
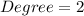
- Since the highest exponent of the denominator is 1:
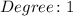
4. Since the degree of the numerator is greater than the degree of the denominator by 1, you can determine that there is no Horizontal Asymptote.
Then, the steps to graph the function are:
• Draw the Vertical Asymptote on the Coordinate Plane (this must be a dotted line or a dashed line).
,
• Find the x-intercept as follows:
Substitute this value of "y" into the function and solve for "x":
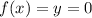
Then:
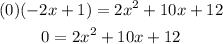
Notice that you need to use the Quadratic Formula to find the x-values:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Then:
![\begin{gathered} x=\frac{-10\pm\sqrt[]{(10)^2-(4)(2)(12)}}{2\cdot2} \\ \\ x_1=-2 \\ x_2=-3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/klios6ahe0gtkbioimr61ctn82ud3uu4r7.png)
Now you know the x-intercepts.
• Find the y-intercept by substituting this value of "x" into the function and evaluating:

Then, you get:
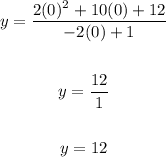
• Now you can find different points on the function by substituting several values of "x" and finding the corresponding y-values.
Then:
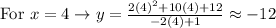

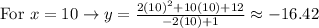
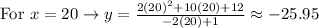
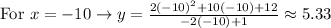
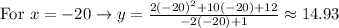
• Finally, plot the points on the Coordinate Plane and graph the function by connecting the points (remember that they must be connected with curves).
Therefore, the answer is (The dashed line is the Vertical Asymptote. There is no Horizontal Asymptote):