Answer:
The effective rate is of 3.87%.
Explanation:
The effective rate, as a decimal, is given by the following formula:
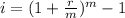
In which r is the nominal rate, as a decimal, and m is the number of compoundings a year.
In this question:
Nominal rate of 3.8%, so r = 0.038
Monthly compounding, so 12 times a year, which means that m = 12. Then
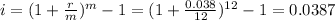
0.0387*100 = 3.87%
The effective rate is of 3.87%.