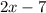You know that the area of the TV can be calculating multiplying its length by its width.
In this case, you know that the area of the TV mentioned in the exercise, is represented by the following expression:
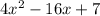
In order to find the expressions that could represend the length and the width (in meteres) of her TV, you need to factor the expression. The steps are shown below:
1. You can identify that the expression has this form:

Where:
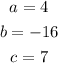
Then, you can rewrite the middle term as the sum of two terms. The product (the result of their multipliplication) of these two terms must be:
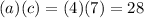
And their sum must be the term coefficient "b":

These two terms would be -14 and -2, because:
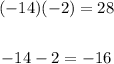
Then, rewriting the expression, you get :
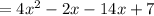
2. Make two groups using parentheses:

3. Factor out the Greatest Common factor of each group:
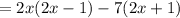
3. Factor out the:

As following:
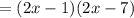
Then you get these expressions:
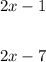
If you give a value to "x" and evaluate:
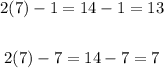
Therefore, the answer is:
- Expression that could represent the length (in meters):
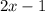
- Expression that could represent the width (in meters):