No, because 3n could be equal to or less than n + 3 (option D)
Step-by-step explanation:
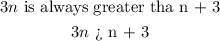
To determine the correct option, we test with different numbers
let n = -3, -1, 0, 3, 4
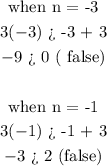
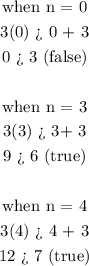
From the above, we can see that depending on the value of n, 3n can be greater than or less than n + 3.
No, because 3n could be equal to or less than n + 3 (option D)