Given
• Amount invested (,P,): $9500
• Annual interest rate (,r,): 10% = 0.1
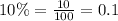
• Accumulated amount (,A,): $19000 because it is double the amount invested.
• Time (,t,): ? years.
Step-by-step explanation
We replace the know values in the below formula, and we solve for t.
![\begin{gathered} A=Pe^(rt) \\ 19000=9500e^(0.1t) \\ \text{ Divide by 9500 from both sides} \\ (19000)/(9500)=(9500e^(0.1t))/(9500) \\ 2=e^(0.1t) \\ \text{ Apply natural logarithm from both sides} \\ \ln(2)=\ln(e^(0.1t)) \\ \text{ Applt the property }\ln(e^x)=x,\text{ for x > 0} \\ \ln(2)=0.1t \\ \text{ Divide by 0.1 from both sides} \\ \frac{\operatorname{\ln}(2)}{0.1}=(0.1t)/(0.1) \\ 6.9\approx t \\ \text{ The symbol }\approx\text{ is read 'approximately'} \end{gathered}]()
Answer
The time it takes to obtain the accumulated amount is approximately 6.9 years.