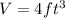Given the dimensions of the carton:
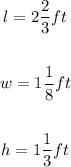
You can convert them to Improper Fractions as follows:
- Multiply the whole number part by the denominator.
- Add the result to the numerator.
- The denominator does not change.
Then:
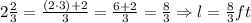
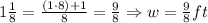
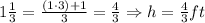
Now you need to use the following formula for calculating the volume of a rectangular prism:
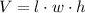
Where "l" is the length, "w" is the width and "h" is the height.
Then, substituting values into the formula and evaluating, you get:
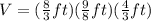
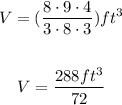
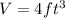
Hence, the answer is: