Find the three arithmetic means between -4 and 16

Question

asked Feb 28, 2023 235k views

1 Answer

Aldanor · Answer 1 · 2023-03-06T08:59:41+0000

SOLUTION

This question simply means we should find the three terms between the -4 and 6 to make this an arithmetic sequence

Let x, y and z be these 3 terms or arithmetic means.

So the arithmetic sequence will be

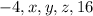
Let d be the common difference, so

From nth term of an arithmetic sequence

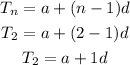
$\begin{gathered} T_n=a+(n-1)d \\ T_2=a+(2-1)d \\ T_2=a+1d \end{gathered}$

So x will be

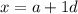
Hence, y and z becomes

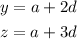
$\begin{gathered} y=a+2d \\ z=a+3d \end{gathered}$

And the 5th term which is 16 will be given as

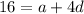
Now note that the first term a = -4. From the equation above the common difference d becomes

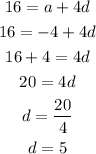
$\begin{gathered} 16=a+4d \\ 16=-4+4d \\ 16+4=4d \\ 20=4d \\ d=(20)/(4) \\ d=5 \end{gathered}$

The common difference is 5,

Hence x is

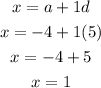
$\begin{gathered} x=a+1d \\ x=-4+1(5) \\ x=-4+5 \\ x=1 \end{gathered}$

y becomes

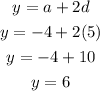
$\begin{gathered} y=a+2d \\ y=-4+2(5) \\ y=-4+10 \\ y=6 \end{gathered}$

z becomes

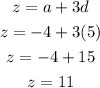
$\begin{gathered} z=a+3d \\ z=-4+3(5) \\ z=-4+15 \\ z=11 \end{gathered}$

Hence, the answer is 1, 6 and 11