Ok the first thing we have to do is calculate the approximate values of each number's probability. That probability tells how often will the dice land on a certain number. To approximate it you have to divide every frequency by the total amount of times the dice was tossed. Let's do that for every number:

Now we can solve the question. For example if you want to know how many times the dice is expected to land on 4 you just need to multiply the probability for that number, which I called P(4), for the total amount of times the dice was tossed, which are 180 times:
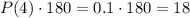
And that's the answer for a.
For item b we need to make more operations. We are being asked how many times the dice is expected to land on a number greater than 3. For this we'll have to use the probability for all the numbers on the dice that are greater than 3: 4, 5 and 6. We'll need to add all these probabilities and multiply the result od that sum by 180:
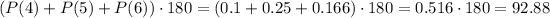
Since 92.88 isn't a whole number we round it to 93 and that's the answer for item b.
We can repeat our calculations for item c but using the probabilities of the even numbers instead. Said numbers are 2, 4 and 6:
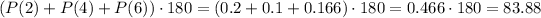
Rounding 83.88 we have 84, the solution to item c.