Answer:
18 sides
Step-by-step explanation:
The sum of the interior angle of a polygon is determined using the formula:
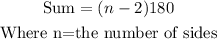
Therefore, we have that:
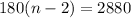
Begin solving the equation for n by dividing both sides by 180.

Next, add 2 to both sides of the equation:
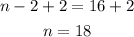
The polygon must have 18 sides.