SOLUTION
Write out the quadratic equation
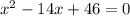
To solve by Completing the square, we apply the following steps
Step1: Take the constant term to the other side
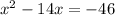
Step2: Get half of the coefficient of x
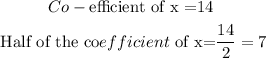
Step3: Square the result in step 2 and add it to the equation in the equation in step1
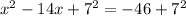
Step4: Factorize the left-hand side and simplify the right-hand side of the equation in step 3
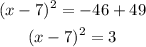
Step5: take the square root of both sides
![\begin{gathered} \sqrt[]{(x-7)^2}=\sqrt[]{3} \\ x-7=\pm\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/p12zcik5rgjpbx2js1qon0pqud37o2q5bg.png)
Hence the value of x is
![\begin{gathered} x=7\pm\sqrt[]{3} \\ \text{Then the two values of x are } \\ x=(7+\sqrt[]{3}),(7-\sqrt[]{3})_{} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9xootxyh7034gbmmi9gkgsct1f1345as4m.png)