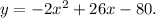Question

If you have 3 points on a parabala from a quadratic equation how do you convert that to a standard form equation?The points are(3,-20)(5,0)(8,0).

Answer 1

The standard form equation of a prabola is

`y=ax^2+bx+c\text{.}`

We are given 3 points of the parabola; (3,-20), (5,0) and (8,0). We'll substitute these values in the standard form equation, which will give us a system of 3 equations we can use to find a, b and c.

From (3,-20) we have:

`-20=9a+3b+c,`
`9a+3b+c=-20.`

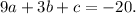
From (5,0):

`0=25a+5b+c,`
`25a+5b+c=0.`

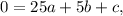
From (8,0):

`64a+8b+c=0.`

So our system of equations is:

`9a+3b+c=-20,`
`25a+5b+c=0,`
`64a+8b+c=0.`

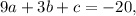
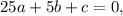
Let's subtract the second equation from the third:

`39a+3b=0.`

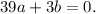
Now let's subtract the first from the second:

`16a+2b=20.`

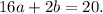
We know have a system of two equations:

`39a+3b=0,`
`16a+2b=20.`

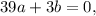
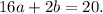
Let's multiply the first by 2 and the second by 3:

`78a+6b=0,`
`48a+6b=60.`

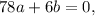
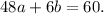
Let's subtract the second from the first:

`30a=-60,`

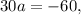
From which, by dividing both sides by 30 we get

`a=-2.`

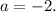
Using this value on either of the equations of the system of two equations will give us the value of b:

`16(-2)+2b=20,`
`-32+2b=20,`
`2b=52,`
`b=26.`

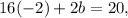
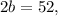
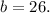
Using the values of a and b in any of the equations of the system of three equations will give us the value of c:

`25(-2)+5(26)+c=0,`
`-50+130+c=0,`
`80+c=0,`
`c=-80.`

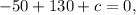
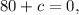
And so, the equation of the parabola in standard from that contains all three given points is:

`y=-2x^2+26x-80.`