Given:
For Juan:
Force, F = 30.0 N
θ = 25.0° above a horizontal line
For his mother:
Force, F = 60.0 N
θ = 35.0° below a horizontal line.
Let's solve for the following:
• (a) What is the magnitude of the vector sum of these two forces?
For Juan, the force(x-component) will be:
Fx = 30 cos(25)i + 30 sin(25)j
For his mother, the force(y-component) will be:
Fy = 60 cos(35)i - 60 sin(35)j
Now, let's find the net force:
Fnet = Fx + Fy
Fnet = 30 cos(25)i + 30 sin(25)j + 60 cos(35)i - 60 sin(35)j
Fnet = 30 cos(25)i + 60 cos(35)i + 30 sin(25)j - 60 sin(35)j
Fnet = 76.338i - 21.736j
To find the magnitude of the vector sum of these two forces, we have:
![F_{\text{net}}=\sqrt[]{(F_x)^2+(F_y)^2}_{}](https://img.qammunity.org/2023/formulas/physics/college/gdtl8wyqptp4kzhdoxnxw34jg8bluhpwkx.png)
![\begin{gathered} F_{\text{net}}=\sqrt[]{(76.338)^2+(-21.736)^2} \\ \\ F_{\text{net}}=79.37\text{ N} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/s81j9lwpyzgpvx184k1i3s98n5v8xxz1x7.png)
Therefore, the magnitude of the vector sum of these two forces is 79.37 N.
• (b) What is the direction of the vector sum of these two forces?
To find the direction of the vector sum of these two forces, apply the formula:

Where:
y-component (Fy) = -21.736
x-component (Fx) = 76.338
Thus, we have:
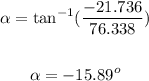
Therefore, the direction of the vector sum of these two forces is at -15.89°
ANSWER:
(a) 79.37 N
(b) -15.89°