Question

I need help solving the quadratic by using the quadratic formula

Answer 1

`x=(2)/(5);x=-(1)/(3)`

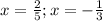
Step-by-step explanation

We want to solve the given quadratic equation by using the quadratic formula:

`15x^2-x-2=0`

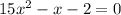
The quadratic formula is:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a = coefficient of x²

b = coefficient of x

c = constant

From the given equation, we have that:

`a=15,b=-1,c=-2`

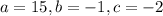
Therefore, solving using the quadratic formula, we have:

`\begin{gathered} x=\frac{-(-1)\pm\sqrt[]{(-1)^2-4(15)(-2)}}{2(15)} \\ x=\frac{1\pm\sqrt[]{1+120}}{30} \\ x=\frac{1\pm\sqrt[]{121}}{30}=(1\pm11)/(30) \\ \Rightarrow x=(1+11)/(30);x=(1-11)/(30) \\ \Rightarrow x=(12)/(30);x=(-10)/(30) \\ x=(2)/(5);x=-(1)/(3) \end{gathered}`

That is the solution of the quadratic equation.