Answer:
(x + 2)/(x - 3) when x is different to 3 and -3.
Step-by-step explanation:
The initial expression is
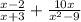
Since (x² - 9) = (x + 3)(x - 3), we get:
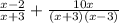
Then, the denominator can't be zero, so x should be different to 3 and to -3. Because
x + 3 = 0 --> x = -3
or
x - 3 = 0 --> x = 3
Then, we can add the fractions as follows
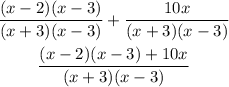
Simplifying, we get
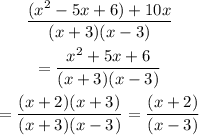
Therefore, the sum is equal to (x + 2)/(x - 3) when x is different to 3 and -3.