Question

Write the following paragraph proof as a two-column proof.

Given: AB = CD and BC = DE
Prove: AC = CE
AB'CD'E
We're given that AB = CD. By the addition property of equality, we add BC to both sides of the equation to get
AB + BC = CD + BC. Since we're also given that BC = DE, we use the subst|tution property of equality to replace BC
with DE on the right side of the equation. So, AB + BC = CD + DE. Next, by segment addition, we get that AB + BC is
equal to AC and that CD + DE is equal to CE. Finally, we use the substitution property of equality on the equation
- AB + BC = CD + DE to replace AB + BC with AC and CD + DE with CE to get that AC = CE

Answer 1

Given:

AB = CD and BC = DE

Required:

We have to prove AB = CD by the two-column method.

Step-by-step explanation:

`Statement.................Reason`
`1.AB=CD\text{ and }BC=DE.................1.Given`

`2.AB+BC=CD+BC.................2.A\text{ddition property.}`

`3.AB+BC=CD+DE.................3.S\text{ubstitution property}`

`4.AC=CE.................4.Segment\text{ addition.}`

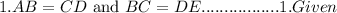
Final answer:

Hence proved AC=CE by the two-column method.

Step-by-step explanation:

Addition property.

The addition property of equality states that when the same quantity is added to both sides of an equation, the equation does not change.

`2.AB+BC=CD+BC.................2.A\text{ddition property.}`

Here we added BC on both sides of the equation, but the equation does not change.

Substitution property.

If BC = DE, then BC can be substituted in for DE in any equation, and DE can be substituted in for BC in any equation.

`3.AB+BC=CD+DE.................3.S\text{ubstitution property}`

Here we have substituted DE for BC in the right of the equation AB+BC=CD+BC.

Segment addtion:

Consider the segments AB, BC, and AC.

The segment AC is split into two segments AB and BC.

By adding AB and BC we get AC.

`AC=AB+BC`

Similarly, consider the segments CD, DE, and CE.

The segment CE is split into two segments CD and DE.

By adding CD and DE we get CE.

`CE=CD+DE`

`4.AC=CE.................4.Segment\text{ addition.}`

Here we have used AC=AB+BC and CE=CD+DE in the equation AB+BC=CD+DE.

Subtraction property:

The subtraction property of equality states that when the same number is subtracted from both sides of an equality, then the two sides of the equation still remain equal.

`A-B=C-B`

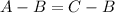
Here we subtracted B from both sides of the equation, but the equation does not change.