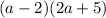Question

Factor out the greatest common factor.(a -2)(a +1)+(a -2)(a + 4)Select the correct choice below and fill in any answer boxes in your choice.O A. (a − 2)(a + 1) + (a − 2)(a + 4) =(Type your answer in factored form.)B. There is no common factor other than 1.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given expression

`(a-2)(a+1)+(a-2)(a+4)`

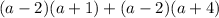
STEP 2: Separate the expression into 2 parts

`\begin{gathered} (a-2)(a+1)---A \\ (a-2)(a+4)----B \\ \text{Expression}=A+B \end{gathered}`

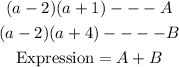
STEP 3: Factorize Part A

`A=(a-2)*(a+1)`

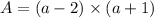
STEP 4: Factorize Part B

`B=(a-2)*(a+4)`

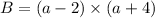
STEP 5: Write out the common factor

`\begin{gathered} \text{Common factor is the factor that can }be\text{ se}en\text{ in both parts of the expression} \\ \text{Common Factor}\Rightarrow(a-2) \\ \\ \text{Factoring out the co}mmon\text{ factor, we have the expression as;} \\ (a-2)\lbrack(a+1)+(a+4)\rbrack \\ \Rightarrow(a-2)\lbrack a+1+a+4\rbrack \\ \Rightarrow(a-2)(2a+5) \end{gathered}`

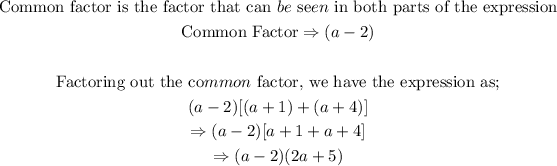
Hence, the correct choice is A and the answer in factored form is:

`(a-2)(2a+5)`