Question

Answer the question by writing an equation and determiningwhether the solutions of the equation are real or non-real.A projectile is launched straight upward from a height of 4 feetwith an initial velocity of 80 feet per second. The height of theprojectile, h, in feet, at time t seconds can be modeled by thefunction h(t)=-16t? +80t +4. Does the projectile reach aheight of 100 feet?

Answer 1

In order to find if the projectile reaches 100 ft of height, let's use h(t) = 100 in the equation and solve it for t:

`\begin{gathered} 100=-16t^2+80t+4 \\ -16t^2+80t-96=0\text{ (:-16)} \\ t^2-5t+6=0 \end{gathered}`

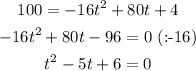
Using the quadratic formula to solve this equation, we have:

`\begin{gathered} a=1,b=-5,c=6 \\ t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t_1=\frac{5+\sqrt[]{25-24}}{2}=(5+1)/(2)=3 \\ t_2=(5-1)/(2)=2 \end{gathered}`

Since we have two valid results of t, the answer is yes, the projectile first reaches 100 meters at t = 2 seconds (when the projectile is going upwards) and then it reaches again when it's going down (at t = 3 seconds).