Question

Julia saved 1 cent ($0.01) on the first day of the month, 2cents ($0.02) on the second day, 4 cents ($0.04) on thethird day and double the previous day's amount on eachsuccessive day Julia's savings for the first five days areshown in the table belowJulia's SavingsDay 1: $0.01Day 2: $0.02Day 3: $0.04Day 4: $0.08Day 5: $0.16on what day will Julia first save an amount greater than$1.00?

Answer 1

The sequence of Julia's savings are a geometric progression, which is a sequence that each term became greter by a constant factor. In this case, que question says that the amount saved doubles each day, starting from $0.01.

If we call a = 0.01 the first term and r = 2 the factor, we can obtain the sum of the amount saved using the formula of the sum of a geometric progression series, which is:

`S_n=(a(r^n-1))/(r-1)`

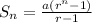
Where S is the sum and n is the number of term. We know a = 0.01, r = 2 and we want to know in which day (n) we get S = 1.00. Thus:

`\begin{gathered} 1.00=(0.01(2^n-1))/(2-1)=0.01(2^n-1) \\ 2^n-1=(1.00)/(0.01)=100 \\ 2^n=100+1=101 \end{gathered}`

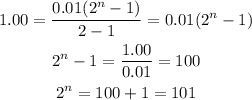
If we see the values of 2^n, we get, for n -> 1,2,3,4,5,6,7...:

2^n -> 2,4,8,16,32,64,128

Or, we can say:

`2^7=128>101`

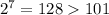
This means that for n = 7, S will be greater than $1.00. We can test that by putting into the formula:

`S_n=(a(r^n-1))/(r-1)=(0.01(2^7-1))/(2-1)=0.01(128-1)=0.01\cdot127=1.27>1.00`

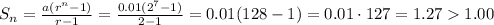
So, we can say that on the 7th day, Julia will first save an amount greater than $1.00.