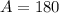The formula for calculate the area of trapezoid is:
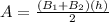
Where "A" is the area of the trapezoid, "h" is the height and the bases are:
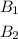
In this case you know that:

In order to find the length of each leg, you need to analyze the figure. See the picture below:
Then, you can identify that:
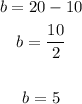
Now you can apply the Pythagorean theorem:
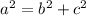
Where "a" is the hypotenuse and "b" and "c" are the legs of the Right triangle.
In this case you can set up that the length of each leg of this trapezoid is "a", and:
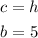
As you can notice, you need the height of the trapezoid and this is unknown. But since you know the perimeter, the bases and you know that the legs have equal length, you can find the length of the legs as following:
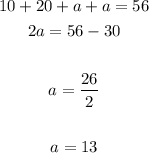
Knowing "a" and "b", you can find "h":
![\begin{gathered} a^2=b^2+c^2 \\ 13^2=5^2+h^2 \\ \sqrt[]{13^2-5^2}=h \\ h=12 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lo9k7jsnv0cvmvifbjd6vaqhlxs1282d0q.png)
Knowing the height you can find the area of the isosceles trapezoid using the formula shown before. Then:
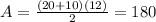
The answers are:
- Length of each leg:

- Height:
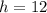
- Area: