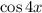Question

Which expression does (cos 3x)(cos x) − (sin 3x)(sin x) simplify to?cos 4xsin 2xcos 2xsin 4x

Answer 1

To simplify the expression, we need to remember that the cosine function has the following identity:

`\cos\alpha\cos\beta-\sin\alpha\sin\beta=\cos(\alpha+\beta)`

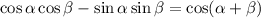
Which gives an expression for the cosine of a sum of angles. In this case we have the following original expression:

`\cos3x\cos x-\sin3x\sin x`

If we compare this expression to the right side of the identity given above, we notice that we have a similar structure but, in this case, instead of alpha we have 3x and instead of beta we have x; for this reason, let:

`\begin{gathered} \alpha=3x \\ \beta=x \end{gathered}`

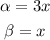
Then we have, according to the identity given above:

`\cos3x\cos x-\sin3x\sin x=\cos(3x+x)=\cos4x`

Therefore, the expression given simplifies to:

`\cos4x`