SOLUTION
First let us graph the function
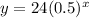
The graph is shown below
(b) After 4 jumps how far will the frog be from the wall
We will substitute x = 4 into the equation, we have

Hence the answer is 1.5 feet
(c) Since the tongue of the frog is 1 inch. And the model was given in feet, we will convert 24 feet to inches, we have
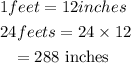
So if the from tongue can reach 1 in. from the wall, we put y = 1 and find x with the new model for inches as

Hence the answer is approximately 8 jumps