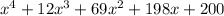Question

Write a polynomial function of least degree with real coefficients in standard form that has the given zeros.–2, –4, –3 + 4i 1) x2 + 6x + 82) x4 + 12x3 + 198x + 2003) x4 + 12x3 + 69x2 + 198x + 2004) x4 + 69x2 + 198x + 200

Answer 1

Given:

The roots of the polynomial funcion are -2, -4 and -3 + 4i.

Step-by-step explanation:

The equation has a complex root, -3 + 4i. So there must be a conjugate complex root of the function. The conjugate of complex root -3 + 4i is -3 - 4i. Thus factor of thr functions are,

`(x+2),(x+4),(x+3+4i)and(x+3-4i)`

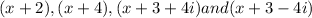
So polynomial function with given factor and with least degree is,

`\begin{gathered} (x+2)(x+4)(x+3+4i)(x+3-4i)=(x+2)(x+4)\lbrack(x+3)^2-(4i)^2\rbrack \\ =(x+2)(x+4)\lbrack x^2+6x+9-16i^2\rbrack \\ =(x+2)(x+4)(x^2+6x+25) \end{gathered}`

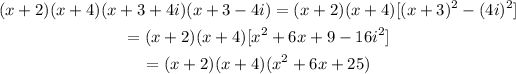
Simplify the equation further.

`\begin{gathered} (x+2)\lbrack x^3+6x^2+25x+4x^2+24x+100\rbrack=(x+2)(x^3+10x^2+49x+100) \\ =x^4+10x^3+49x^2+100x+2x^3+20x^2+98x+200 \\ =x^4+12x^3+69x^2+198x+200 \end{gathered}`

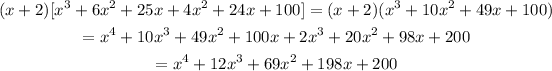
So polynomial function is,

`x^4+12x^3+69x^2+198x+200`