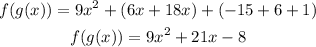The functions are


You have to calculate (f o g)(x), this means that you have to replace g(x) inside f(x) → f(g(x))
So for f(x) x will be g(x) as:
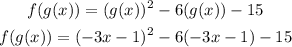
I'll separate the composition in parts and solve them separatelly, once all terms are solved I'll add them together again:
So first solve the square of the binomial:
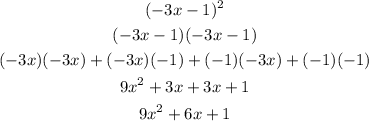
Next solve the second term, by applying the distributive property of multiplication:
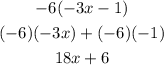
Now put both solutions toghether with the last term of the equation and order the like terms together:
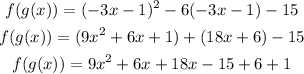
And finally simplify the expression by solving the operations between the like terms: