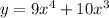
To find the critical points, first we derivate the function:
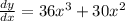
dy/dx has roots x = 0 and x = -5/6.
When x < -5/6, we can check that dy/dx is negative. When -5/6 < x < 0, we can check that dy/dx is positive. And, when x > 0, we can check that dy/dx is also positive.
Therefore, y is increasing when x > -5/6 and decrasing when x < -5/6. y has inflection points at x = -5/6 and x = 0