Question

Prove the polynomial identity.(x+y)^3 = x^3 + y^3 + 3xy(x+y)

Answer 1

To prove this identity, we can start by expending the left side:

`(x+y)^3=(x+y)(x+y)(x+y)`

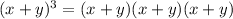
Now, we can apply the distributive property in two of these factors:

`(x+y)(x+y)=x\cdot x+x\cdot y+y\cdot x+y\cdot y=x^2+xy+xy+y^2=x^2+2xy+y^2`

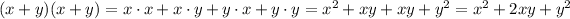
Now, we substitute it back:

`(x+y)^3=(x+y)(x^2+2xy+y^2)`

And now, we can apply the distributive property again:

`\begin{gathered} (x+y)(x^2+2xy+y^2)=x\cdot x^2+x\cdot2xy+x\cdot y^2+y\cdot x^2_{}+y\cdot2xy+y\cdot y^2= \\ =x^3+2x^2y+xy^2+x^2y+2xy^2+y^3=x^3+3x^2y+3xy^2+y^3 \end{gathered}`

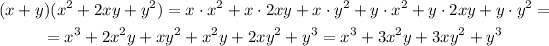
Going back to the equation, we have:

`(x+y)^3=x^3+3x^2y+3xy^2+y^3`

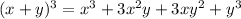
The two middle terms have the factors "3", "x" and "y" in common, so we can factor them out:

`\begin{gathered} (x+y)^3=x^3+3xy(x+y)+y^3 \\ (x+y)^3=x^3+y^3+3xy\mleft(x+y\mright) \end{gathered}`

And we end up with the identity we wantd to prove, so it is proved.