Answer:
7x-10y=57
Explanation:
The following two points are on a line:
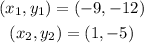
To find the equation of the line, use the two-point formula for the equation of a line.
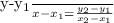
Substitute the given points:
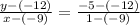
Then simplify:
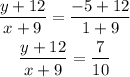
Cross multiply:
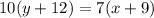
Open the bracket:
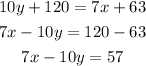
The equation of the line is 7x-10y=57.