A chemist has three different acid solutions.
Let x denotes the first acid, y denotes the second acid, and z denotes the third acid.
The first solution contains 20% acid the second contains 30% acid and the third contains 50% acid
She created 60 liters of a 40% acid mixture using all three solutions.
Mathematically,

The number of liters of 50% solution used is three times the number of liters of 30% solution used.
Mathematically,
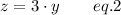
Also, we know that the sum of all solutions must be equal to 60 liters,
Mathematically,
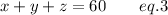
Now let us substitute the eq.2 into the eq.1
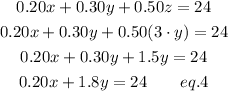
Now let us substitute the eq.2 into the eq.3
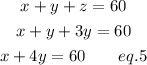
As you can see, we now have 2 equations with 2 unknowns
Let us solve them using the substitution method.
Re-arrange eq.5 for x and substitute it into eq.4
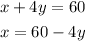
So eq.4 becomes
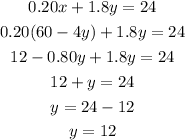
So y = 12 liters.
Now let us substitute y = 12 into eq.5
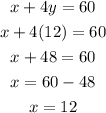
So x = 12 liters
Finally, substitute y = 12 into eq. 2
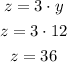
So z = 36 liters
Therefore, the chemist used 12 liters of 20% solution, 12 liters of 30% solution, 36 liters of 50% solution.