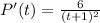
1) Let's calculate the first derivative of this function, making use of the best property:
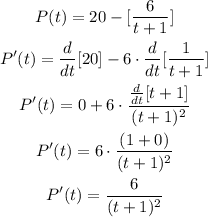
Note that we have differentiated separately the summands pulling out the constant factors, and then used the reciprocal rule and rewrote 6/t+1 as 6*1/t+1.
2) And that is the answer.