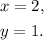Question

.^{2Solve each system of equations without graphing and show your reasoning, Then, check yoursolutions,2x + 3y = 7es 2x + 3y = 7-2x + 4y = 143x – 3y = 3

Answer 1

To solve both systems of equations, we will use the addition method.

A) Adding the given equations, we get:

`2x+3y+(-2x+4y)=7+14.`

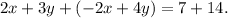
Simplifying the above equation, we get:

`7y=21.`

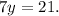
Dividing by 7:

`y=(21)/(7)=3.`

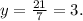
Substituting y=3 in the first equation of the system and solving for x, we get:

`\begin{gathered} 2x+9=7, \\ 2x=-2, \\ x=-1. \end{gathered}`

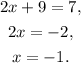
Answer part A:

`\begin{gathered} y=3, \\ x=-1. \end{gathered}`

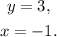
B) Adding the two equations of the system, we get:

`2x+3y+(3x-3y)=7+3.`

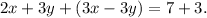
Simplifying the above equation, we get:

`5x=10.`

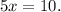
Dividing by 5, we get:

`\begin{gathered} 5x=10, \\ x=(10)/(5), \\ x=2. \end{gathered}`

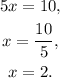
Substituting x=2 in the second equation of the system, we get:

`\begin{gathered} 3(2)-3y=3, \\ 6-3y=3. \end{gathered}`

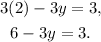
Subtracting 6 from both sides of the equation, we get:

`\begin{gathered} 6-3y-6=3-6, \\ -3y=-3. \end{gathered}`

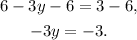
Dividing by -3, we get:

`\begin{gathered} (-3y)/(-3)=(-3)/(-3), \\ y=1. \end{gathered}`

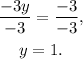
Answer part B:

`\begin{gathered} x=2, \\ y=1. \end{gathered}`