Question

Drag and drop the slope and y-intercept into the corresponding boxes what is the slope and y-intercept of the line?

Answer 1

Since all points lie on the same line, we can use any two of them to calculate the slope of this line.

Given two points, the slope is:

`m=(y_2-y_1)/(x_2-x_1)`

Let's use the first two rows. Assuming the question wants h in the x-axis and c in y-axis, we have: (0, 432) and (3, 288). So:

`\begin{gathered} m=(288-432)/(3-0) \\ m=(-144)/(3) \\ m=-48 \end{gathered}`

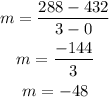
And for the y-intercept, it is the y value for when x = 0. Since h is the x-axis, we need to look for h = 0, which is the first row. The corresponding c value is 432, which is the y-intercept.

Thus, the slope is -48 and the y-intercept is 432.