To answer this question, we need to find the number of cases for which the sum of a pair of dice is odd and more than 8:
We add the value of the possible values of the dice at the bottom, and at the left. Then, we sum the values for 1 (bottom) and 1 (left) = 2, 1 (bottom) and 2 (left) = 3, and so on until we complete the sum for each of the cases.
As we can see from the above "matrix", we can see the sum of both dice. We have 6 * 6 = 36 possible cases (the sample space). Then, we have the cases when the sum is odd and more than 8 are the following cases:
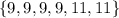
And these are 6 cases (we did not count 10 and 12 because their sum is obviously even). Then, the probability of a sum that is odd and more than 8 is, then:
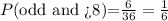
Therefore, this probability is equal to 1/6.