Given:
An architect has designed two tunnels.
Tunnel A is modeled by:
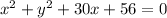
Tunnel B is modeled by:
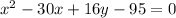
Part A: write the equation of tunnel A in standard from
So, we will complete the square for the two variables x, and y as follows:
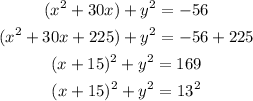
So, the answer to part A:
The equation will be: (x+15)² + y² = 13²
The conic section is: Circle with canter (-15, 0) and radius = 13 feet
Part B: Write the equation of tunnel B in standard from
So, we will complete the square for the variable x as follows:
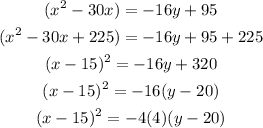
So, the answer to part B:
The equation will be: (x-15)² = -4(4)(y-20)
The conic section is: a Parabole with the vertex at (15, 20)
Part C: Determine the maximum height of each tunnel.
Tunnel A:
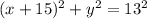
So, the radius = 13, so, the diameter = 2 * 13 = 26
So, the maximum height = 13 feet
The truck has a height = of 13.5 feet
so, it will not be able to pass through the tunnel A
Tunnel B:
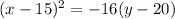
when y = 0, solve for x:
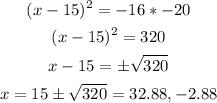
When x = 15, we will find the maximum height

So, the maximum height = 20 feet
the truck will be able to pass through the tunnel