Question

A coffee shop offers 10 different types of flavor shots. If customer can choose any number of flavor shots to have in their coffee, how many flavor shot combinations are possible?

Answer 1

Given that the coffee shop offers 10 different types of flavor shots. If the customer can choose any number of flavor shots we need to find how many flavors shot combinations are possible.

Step-by-step explanation

Since we are looking at the possible flavor shots combinations, this implies that the customer must pick at least one flavor shot out of the possible combination.

Therefore we sum up all the possibilities of selecting a flavor shot for the customer's coffee. This is given as;

`\begin{gathered} ^(10)C_1+^(10)C_2+^(10)C_3+.\ldots^(10)C_(10) \\ For\text{ combination we have;} \\ ^nC_r=(n!)/((n-r)!r!) \\ \therefore^(10)C_1+^(10)C_2+^(10)C_3+.\ldots^(10)C_(10) \\ =10+45+120+210+252+210+120+45+10+1=1023 \end{gathered}`

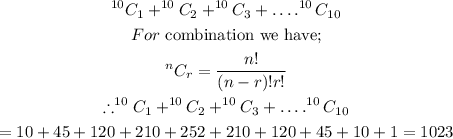
Answer: 1023