SOLUTION
From

So the x-intercepts are the roots of the equation, which is -2 or 4
Since x = -2 or x = 4
Now let's find the y-intercept
Since x-square is positive, there is a minimum value, that is there is a lowest point
We find the lowest point by finding the derivative of y with respect to x
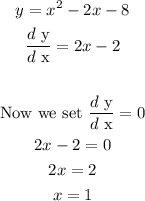
So the lowest value for y is
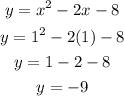
So, the lowest value of y = -9