40320
Step-by-step explanation:
In the word triangle, there are no repetition of of letters
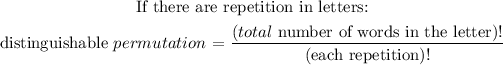
This means the distinguishable permutation of the letters = (total number of letters)!
total number of letters = 8
the distinguishable permutation of the letters = 8!
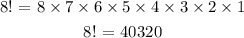
the distinguishable permutation of the letters = 40320