Question

Tickets for a raffle cosr $7. There were 643 tickets sold. One ticket will be randomly selected as the winner, and that person wins $1800 and also the person is given back the cost of the ticket. For someone who buys a ticket, what is the Expected Value (the mean of the distribution)? If the Expected Value is negative, be sure to include the "-" sign with the answer. Express the answer rounded to two decimal places.Expected Value = $ _______

Answer 1

$-4.18

Explanation:

The expected value would be a subtraction between the products of the probabilities of winning and losing with their respective prizes.

in case of winning where the probability is 1 among the total number of tickets sold, the prize is the value of the ticket plus $1800

But in case of losing, the 7 dollars are lost, the probabilities would be the total of the tickets minus 1 divided by the total of tickets

Given:

P (winning) = 1/643

P (losing) = 642/643

Therefore:

`\begin{gathered} E=(1)/(643)\cdot(7+1800)-7\cdot(642)/(643) \\ E=2.81-\: 6.99 \\ E=-4.18 \end{gathered}`

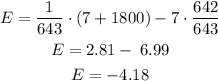
Therefore, the expected value is $-4.18