ANSWER:
The length is 10 feet where the width is 2 feet.
Step-by-step explanation:
Let l represent the length of the rectangle
Let w represent the width of the rectangle
From the question, we have;
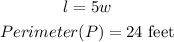
Recall that the formula for the perimeter(P) of a rectangle is given as;
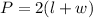
Let's now substitute P with 24 and l with 5w in the above equation and solve for w as seen below;
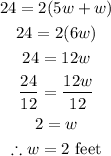
So the width of the rectangle is 2 feet
The length of the rectangle can be determined as seen below;
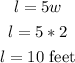
So the length of the rectangle is 10 feet