Given:
The perimeter of a rectangle, P=168 in.
Let w be the width and l be the length of the rectangle.
The length of the rectangle is three times its width.
Therefore,
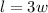
Now, the perimeter of the reactnagle can be expressed as,
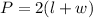
Put l=3w and P=168 in the above equationa and solve for w.
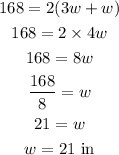
Now, the length of the rectangle is,
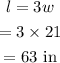
Therefore, the length of the rectangle is 63 in and the width of the rectangle is 21 in.