Question

Solve each system by graphing. Tell whether the system has one solution, indefinitely many solutions, or not solutions. (I'll send the image)

Answer 1

The equation of a line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

You have the first equation:

`y=-2x+1`

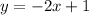
You can identify that:

`\begin{gathered} m_1=-2 \\ b_1=1 \end{gathered}`

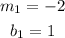
Knowing the slope and the y-intercept, you can graph the first line.

The second equation is:

`y=-(2)/(3)x+5`

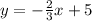
Notice that:

`\begin{gathered} m_2=-(2)/(3) \\ \\ b_2=5 \end{gathered}`

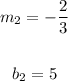
Knowing the slope and the y-intercept, you can graph the second line.

The graph is:

Since the lines intersect each other, then the System of equations has one solution. The solution is the point of intersection.

The answer

It has One solution:

`(-3,7)_{}`

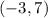
Graph: