Question

g(x)= -16x2 + 64x + 80 where x is the number of seconds after the rocket is launched. The function can also be written in factored form as g(x) = -16 (x + 1)(x - 5).When does the rocket hit the ground?

Answer 1

The equation given that describes the movement of the rocket is given by:

`g(x)=-16x^2+64x+80`

The sketch of the path of the rocket is shown when we plot this equation:

Thus, if we are to find when the rocket touches the ground, we simply need to find the roots of the quadratic equation.

In order to find the roots, we first factorize the quadratic equation. The factorized form

of the equation has already been given to us as:

`g(x)=-16(x+1)(x-5)`

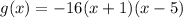
Hence, we can easily find the roots of the equation by equating the expressions of x to zero:

`\begin{gathered} x+1=0 \\ or \\ x-5=0 \\ \\ \therefore x=-1 \\ x=5 \end{gathered}`

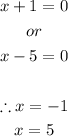
Therefore, the rocket must hit the ground at time: x = 5 since time cannot be negative.

Therefore, the final answer is:

x = 5