Question

Balance the following equation by entering the lowest whole number coefficients for each substance. This includes the number 1 for substances with coefficients of 1.

Answer 1

We have to have the same number of atoms of each species in both sides of the reaction.

Lets call:

a: mols of H3PO4

b: mols of P2O5

c: mols of H2O

Balance for hydrogen H:

`a\cdot3=c\cdot2`

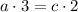
Balance for Phosphorus P:

`a\cdot1=b\cdot2`

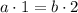
Balance for Oxygen O:

`a\cdot4=b\cdot5+c\cdot1`

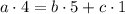
We can express a b in function of c, and then solve backwards:

`3a=2c\longrightarrow a=(2)/(3)c`
`a=2b\longrightarrow b=(1)/(2)a=(1)/(2)\cdot(2)/(3)c=(1)/(3)c`

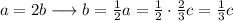
This system has infinite solutions. The third equation gives an identity, so we must fix a value for c and then calculate the others.

As b and c are "thirds" of c, we select c=3.

Then:

`\begin{gathered} a=(2)/(3)c=(2)/(3)\cdot3=2 \\ b=(1)/(3)c=(1)/(3)\cdot3=1 \end{gathered}`

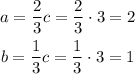
As b=1, we know that is the lowest possible combination of integers:

Answer:

- 2 mols of H3PO4

- 1 mol of P2O5

- 3 mols of H2O