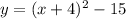Solution:
Given:
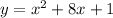
The vertex form of a quadratic equation is given by;
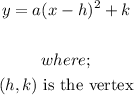
Using a graph plotter to get the vertex of the parabola,
The vertex is at (-4,-15) and the curve passes through the point (0,1)
Hence,
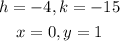
Substituting these points into the equation for the vertex form of a parabola;

Therefore, the equation in vertex form is;