Question

I need help with this problem from my trigonometry prep guideIt asks to solve (a) and (b) Please put these separately so I know which is which

Answer 1

Part 1. We are given the following expression:

`(3x^5-(1)/(9)y^3)^4`

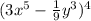
This is an expression of the form:

`(a+b)^n`

This expression can be expanded using the binomial theorem as follows:

`(a+b)^n=\sum ^n_(k\mathop=0)(n!)/((n-k)!k!)a^(n-k)b^k`

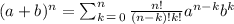
In this case, we have:

`\begin{gathered} a=3x^5 \\ b=-(1)/(2)y^3 \\ n=4 \end{gathered}`

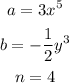
Substituting in the binomial theorem:

`(3x^5-(1)/(2)y^3)^4=\sum ^4_{k\mathop{=}0}(4!)/((4-k)!k!)(3x^5)^(4-k)(-(1)/(2)y^3)^k`

Part 2. To determine the terms of the binomial we will expand the sum. To do that we will use the values of "k" from 0 to 4:

`\sum ^4_{k\mathop{=}0}(4!)/((4-k)!k!)a^(4-k)b^k=(4!)/((4-0)!0!)a^(4-0)b^0+(4!)/((4-1)!1!)a^(4-1)b^1+(4!)/((4-2)!2!)a^(4-2)b^2+(4!)/((4-3)!3!)a^(4-3)b^3+(4!)/((4-4)!4!)a^(4-4)b^4`

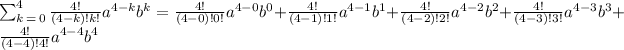
Now, we solve the coefficients and the exponents:

`\sum ^4_{k\mathop{=}0}(4!)/((4-k)!k!)a^(4-k)b^k=a^4+4a^3b^{}+6a^2b^2+4a^{}b^3+b^4`

Now, we substitute the values of "a" and "b":

`\sum ^4_{k\mathop{=}0}(4!)/((4-k)!k!)(3x^5)^(4-k)(-(1)/(2)y^3)^k=(3x^5)^4+4(3x^5)^3(-(1)/(2)y^3)+6(3x^5)^2(-(1)/(2)y^3)^2+4(3x^5)(-(1)/(2)y^3)^3+((1)/(2)y^3)^4`

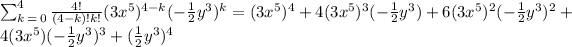
Now, we simplify each term:

`\sum ^4_{k\mathop{=}0}(4!)/((4-k)!k!)(3x^5)^(4-k)(-(1)/(2)y^3)^k=81x^(20)-12x^(15)y^3+(2)/(3)x^(10)y^6-(4)/(243)x^5y^9+(1)/(6561)y^(12)`

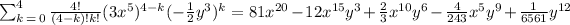
And thus we get the simplified terms.