Question

Given rectangle ABCD, where AB = 5, BC = 24. AE is drawn such that E is the midpoint of BC. If F is the point of intersection of BD and AE, find the length of FE. Draw a diagram.

Answer 1

Consider the schematic diagram below,

Given that E is the mid point of BC,

`BE=EC`

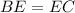
The side BC measures 24 units, then it follows that,

`\begin{gathered} BE=(BC)/(2)=(24)/(2)=12 \\ \Rightarrow BE=EC=12 \end{gathered}`

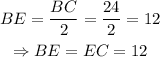
It is known that the angle between two adjacent sides of a rectangle is 90 degrees. So the triangle BCD will be a right triangle.

In the triangle BCD,

`\begin{gathered} \angle CBD=\tan ^(-1)((CD)/(BC))^{} \\ \angle CBD=\tan ^(-1)((5)/(24)) \\ \angle CBD\approx11.77^(\circ) \end{gathered}`

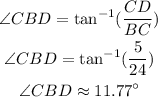
Similarly, in the right triangle ABE,

`\begin{gathered} \angle AEB=\tan ^(-1)((AB)/(BE))^{} \\ \angle AEB=\tan ^(-1)((5)/(12)) \\ \angle AEB\approx22.62^(\circ) \end{gathered}`

Theorem: The sum of internal angles of a triangle is 180 degrees.

Applying this theorem in triangle BFE,

`\begin{gathered} \angle BFE+\angle FBE+\angle FEB=180 \\ \angle BFE+11.77+22.62=180 \\ \angle BFE=180-22.62-11.77 \\ \angle BFE\approx145.61 \end{gathered}`

Now, apply the sine rule in the triangle BFE,

`\begin{gathered} (BF)/(\sin\angle BEF)=(FE)/(\sin\angle FBE)=(EB)/(\sin \angle BFE) \\ (BF)/(\sin 22.62)=(FE)/(\sin(11.77))=(12)/(\sin(145.61)) \\ (BF)/(\sin22.62)=(FE)/(\sin(11.77))=21.24 \end{gathered}`

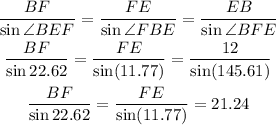
It follows that,

`\begin{gathered} FE=21.24*\sin (11.77) \\ FE=21.24*0.204 \\ FE\approx4.33 \end{gathered}`

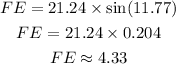
Thus, the length of the side FE is 4.33 units, approximately.