The system of inequalities can be plotted using a graphing calculator. The graph of the system of inequalities is shown below:
The solution to the system of equations is given to be the unshaded region.
The objective function is given to be:
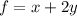
The constraints of the graph of the system of inequalities are shown in the diagram below:
The constraints are:
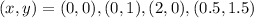
The values of f at the constraints are calculated as follows:
At (0, 0)
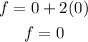
At (0, 1)
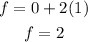
At (2, 0)
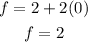
At (0.5, 1.5)
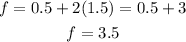
Therefore, the maximum can be gotten at (0.5, 1.5).