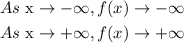Question

How do I find the relative extrema of the polynomial and the end curve behavior?

Answer 1

Given the function below

`y=(1)/(3)x^5-2x^4+\cdots+x-6`

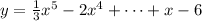
The end behavior of a function describes it behavior as x approaches +∞ and -∞

The leading term of the given function is

`\begin{gathered} (1)/(3)x^5 \\ \text{And the degree is 5 which is odd} \\ The\text{ leading coefficient is positive }(1)/(3) \end{gathered}`

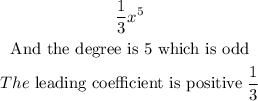
Where f(x) = y

When x approaches to -∞, f(x) approaches -∞ and when x approaches +∞, f(x) approaches +∞

Hence, the answer is

`\begin{gathered} As\text{ x}\rightarrow-\infty,f(x)\rightarrow-\infty \\ As\text{ x}\rightarrow+\infty,f(x)\rightarrow+\infty \end{gathered}`